Pressure and flow in pipelines are two important parameters for industrial processes. Pressure or differential pressure, flow rate, and pipe diameter are all related. For example, Bernoulli equation, Poiseuille equation, etc., all try to sort out the relationship between pipeline flow, pressure, and pipe diameter.
It is important to monitor pressure and flow in pipelines, they directly affect the performance and safety of your fluid system! So, let’s take a look at their relationship.
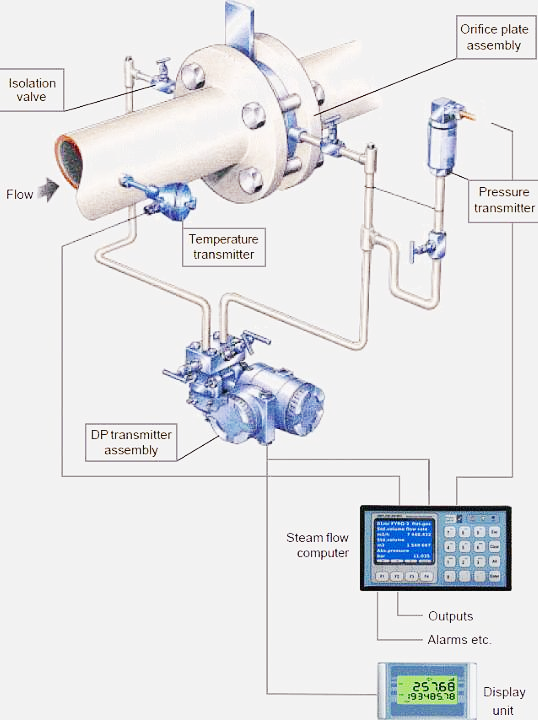
Basic concepts:
To understand the relationship between flow and pressure, we need to understand what flow and pressure are, and the definition of pipe diameter.
What is Pressure?
“Pressure” is a continuous physical force exerted on an object it comes into contact with. What we are talking about here is the pressure of the fluid in the pipe.
Of course, others include tank pressure, gas pressure, etc. You may refer to: Difference Between Static Pressure, Dynamic Pressure And Total Pressure
What is Flow?
In the pipeline system, pipeline flow refers to the amount of fluid passing through a certain section of the pipeline per unit time.
Typically, flow can be expressed in terms of volume flow or mass flow.
Volume flow refers to the volume of fluid flowing through a pipe cross-section per unit time, usually expressed in units such as cubic meters per second (m³/s) or cubic meters per hour (m³/h).
Mass flow refers to the mass of fluid flowing through a pipe section per unit time, usually expressed in units such as kilograms per second (kg/s).
More about: Key Differences Between Mass Flow Rate And Volumetric Flow Rate
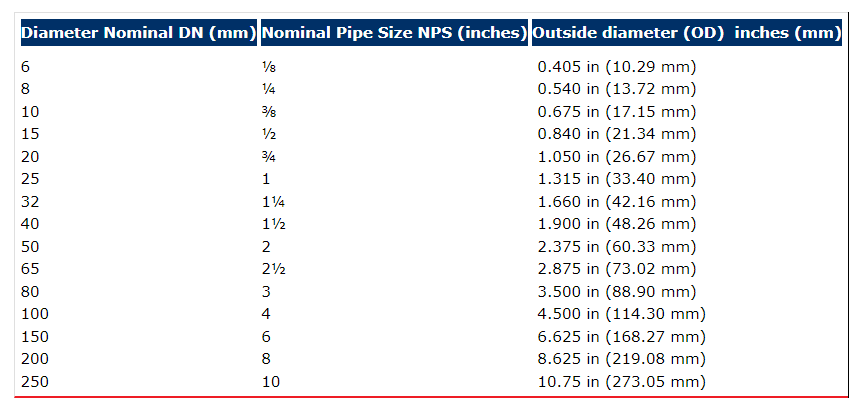
What is Pipe Diameter?
Pipe diameter refers to the size of the pipe, which may be the inner diameter (ID), outer diameter (OD), or nominal diameter (DN).
In pipeline engineering and fluid transmission, pipe diameter directly affects the flow efficiency of fluid and the carrying capacity of the pipeline.
Of course, we use DN more often. It facilitates the unification of pipe size standards globally, making our flow meters and other products compatible with pipe products produced in different countries.
Relationship between flow and pressure
No equation alone can encompass the relationship between pressure and flow of a fluid in motion. Different applications and conditions may involve different types of equations. Here we briefly discuss two different common equations related to pressure and flow: Bernoulli’s equation and Poiseuille’s law.
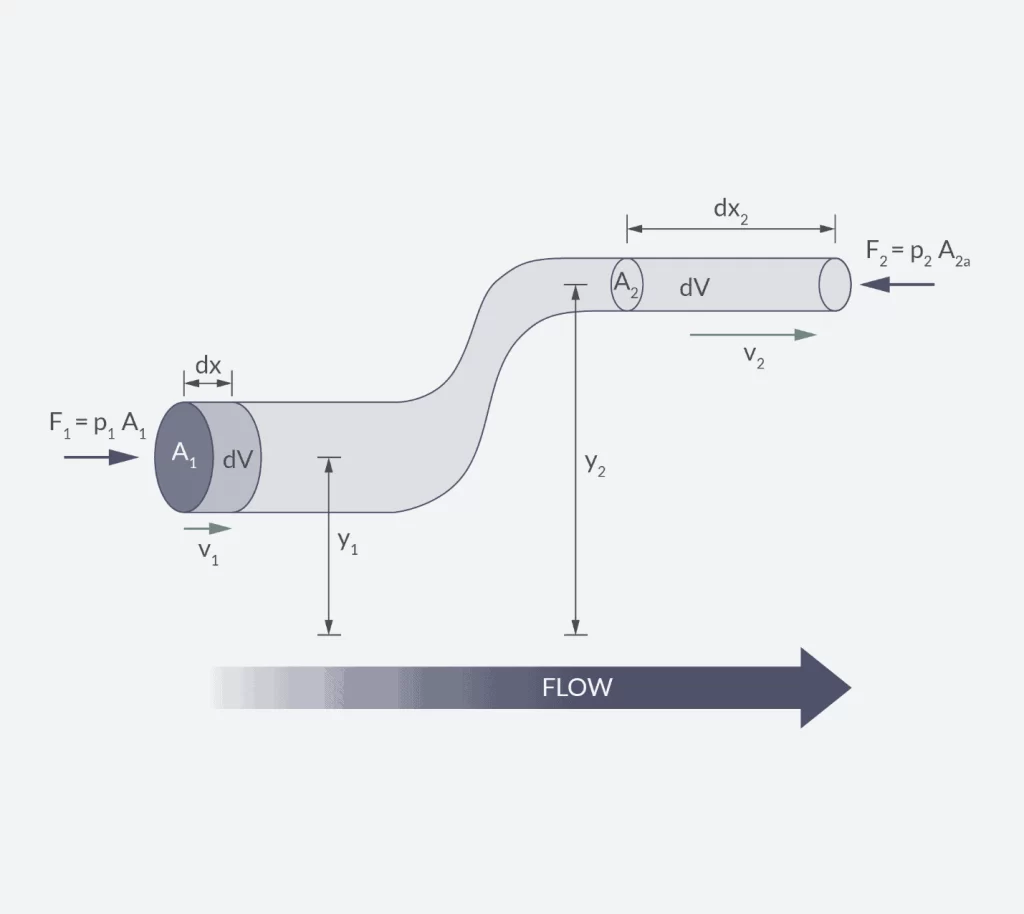
Bernoulli Equation
Bernoulli’s equation is a fundamental principle in fluid mechanics that describes the relationship between flow velocity, pressure, and height in an ideal fluid (that is, an incompressible and frictionless fluid). The general form of the equation is as follows:
P + ½ρv² + ρgh = constant.
in:
P represents the pressure of the fluid,
ρ is the density of the fluid,
v is the velocity of the fluid,
g is the acceleration due to gravity,
ℎ is the height of the fluid relative to the reference point.
When considering two different points on the same pipeline, the equation can be expressed as:
P₁ + ½ρv₁² + ρgh₁ = P₂ + ½ρv₂² + ρgh₂.
The relationship between pressure, flow and pipe diameter:
- Pressure and flow rate: Bernoulli’s equation states that an increase in the flow rate of a fluid causes a decrease in its pressure and vice versa. This means that if a fluid accelerates in a pipe, its pressure will decrease accordingly.
- Flow and Pipe Diameter: Flow (usually volumetric flow) is the product of the fluid velocity and the cross-sectional area through which it flows. According to Bernoulli’s equation, if the pipe diameter decreases, in order to maintain the same flow rate, the flow rate must increase, which will cause the pressure to decrease.
- Effect of height difference: The ρgh term in the equation represents the potential energy of the fluid, taking into account the effect of height difference on fluid pressure and velocity.
Differential pressure flowmeters are device that use the principle of Bernoulli’s equation to measure fluid flow. A pressure difference is created before and after the throttling device. By measuring this pressure difference and combining the characteristics of the pipe and fluid, the flow rate of the fluid can be calculated. Common ones include orifice plates, venturis, nozzles, and any structure that makes it easy to measure differential pressure.
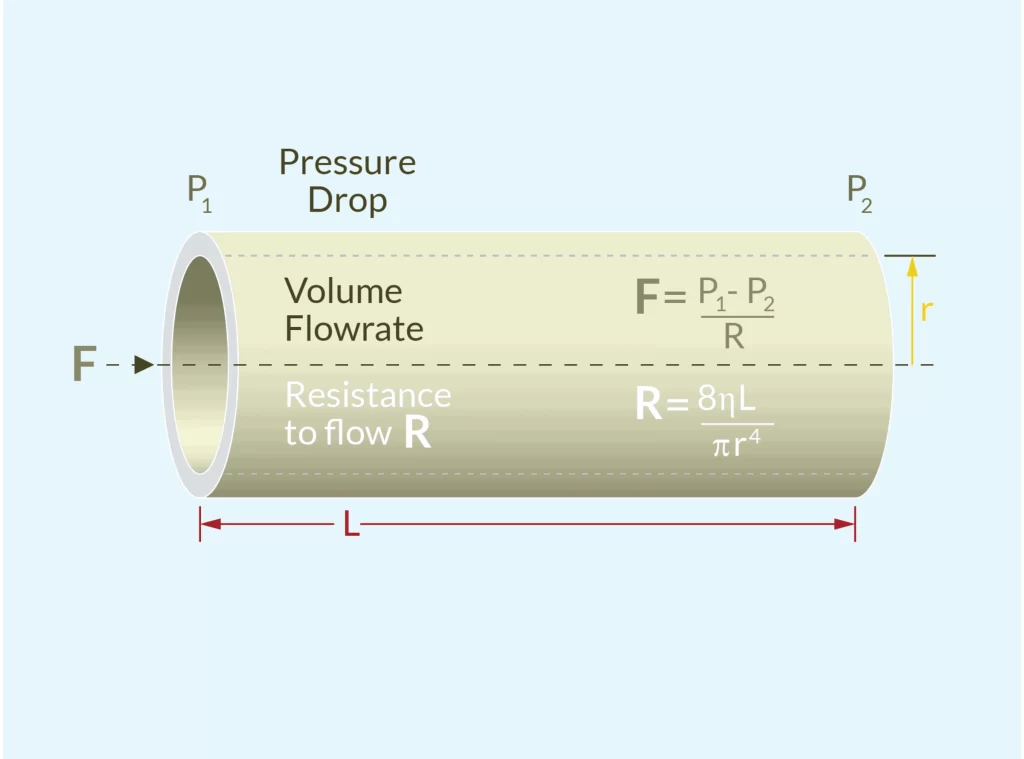
Poiseuille’s Law
Poiseuille’s law applies to laminar flow of viscous fluids in pipes. It describes the relationship between flow rate, pressure gradient and pipe diameter.
The formula is: Q = π(P₁ – P₂)r⁴ / 8μL.
in:
Q is the volumetric flow rate,
P1 and P2 are the pressures at both ends of the pipe,
r is the radius of the pipe,
μ is the viscosity of the fluid,
L is the length of the pipe.
The relationship between pressure, flow and pipe diameter:
Pressure and flow: Poiseuille’s law states that flow is proportional to the pressure difference. The greater the pressure difference, the greater the flow in the pipe.
Pipe diameter and flow rate: Flow rate is proportional to the fourth power of pipe diameter, which means that small changes in pipe diameter can cause significant changes in flow rate. As the pipe diameter increases, the flow rate increases significantly.
Bernoulli’s equation and Poiseuille’s law describe the movement of fluid in pipelines from different perspectives. Through these two equations, the complex relationship between pressure, flow rate and pipe diameter in the pipeline system can be understood and calculated. Bernoulli’s equation is more applicable to ideal fluids and high-speed flows, while Poiseuille’s law is applicable to laminar flow states of viscous fluids.
Featured online calculate Tools
In addition to calculating it ourselves, there are actually a variety of online calculators that can calculate flow and pressure based on our various input parameters (such as pipe diameter, fluid type, and velocity).
For example: Copely can easily calculate the average volumetric flow rate of a fluid by changing each of three variables: length, pressure, and pore size.
The impact on the predicted traffic is then given in three graphs, where two variables are held constant and the traffic is plotted against a range of values for the third variable.
And, GIGAcalculator supports easily calculating the volumetric flow rate (aka discharge) of a pipe given the size of the pipe and the pressure difference between the two ends of the pipe or the velocity of the liquid or gas flowing through the pipe. The flow calculator can also calculate the mass flow rate of a fluid given the density of the fluid.
When calculating and measuring fluid flow using Bernoulli’s equation or Poiseuille’s law, you may encounter problems such as turbulence and pressure loss.
Featured Pressure Sensors and Flow Meters
- Top 4 Types of Pipeline Flow Meters-DN6~DN1000~DN6000
- Flow Measurement 101
- Pressure Transducer Troubleshooting: Expert Insights & Tips
- Fluid Pressure Guide: Static Pressure Vs. Dynamic Pressure Vs. Total Pressure
- Steam Pressure Sensor/transducer for Industrial Steam Measurement
- What Is Solvent Flow Meter? Industrial Selection Guide
- What Is a BTU Meter? | BTU Energy Measurement Systems
- Mechanical Flow Meter 101-Mechanical Flowmeters Selection Guide
- Bidirectional Flow Meters | Electromagnetic, Ultrasonic, Mass and Porous Orifice Flowmeter
- Volumetric Flow Meters: Comprehensive Guide and Product List
The relationship between pressure and flow is complex. Through Bernoulli’s equation and Poiseuille’s law, we can reveal the basic dynamic principles of fluid movement in pipes. However, the emergence of practical problems such as turbulence and pressure loss reminds us that more careful considerations and precise operations are needed in practical applications.
Accurate understanding and calculation of flow-pressure relationships is critical to ensuring efficient and safe operation of piping systems. We hope that this article can provide valuable reference and guidance for your work in this field. If you need related pressure transmitters or flow meters, you can contact our sales engineers at any time!
-1.jpg)







