Relationship Between Pressure And Flow Rate: Key Insights

When the pressure in a pipe increases, does the flow rate also increase? Does the diameter of the pipe matter when calculating the flow rate?

Qualitative investigation suggests a proportionate link between pipe pressure and flow rate. Assume a pipeline with a single pressure source at one end. The amount of Water flow meter that shoots out of a faucet depends on the pressure in the pipe.

This blog post delves into key aspects of pressure-flow relationships, focusing on the pressure drop in Coriolis flow meters and orifice plates.

RFQ

Why Are Flow And Pressure Important?

Monitoring flow and pressure is essential in the following applications:

Monitoring and controlling water in taps;
Dosing chemicals to water treatment systems;
Leakage detection and reduction;
Monitoring water consumption in commercial and residential buildings;
Monitoring discharge water and influent water quantity;
Monitoring the flow of water between reservoirs;

Relationship between Flow Rate And Pressure

From the perspective of qualitative analysis, the relationship between the pressure in the pipe and the flow rate is directly proportional; the greater the pressure, the higher the flow rate.

Flow And Pressure: Bernoulli’s Equation

Daniel Bernoulli initially introduced the concept of low-velocity high-pressure in a stream in 1726. A low-pressure situation occurs when the velocity is high. That’s what Bernoulli’s principle is all about.

Before developing the continuous medium theory in fluid mechanics, this was the guiding concept of hydrodynamics. The fundamental principle is the principle of energy conservation in fluid mechanics. That is, the sum of the energies of motion, gravity, and pressure remains unchanged.

As a result, it can only be used with perfect fluids with an infinite density and zero viscosity. Bernoulli’s principle uses the following equation: p+1/2ρv2+ρgh=C

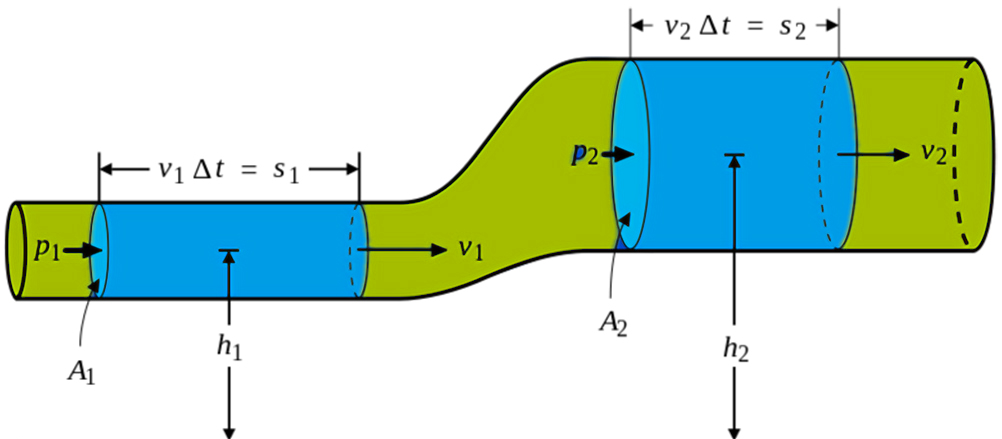
Where:
p = The pressure in the fluid
v = The fluid’s flow velocity
ρ = The density of the fluid
g = The acceleration of gravity
h = The height of the point/horizontal drop
C = The constant

For Bernoulli’s principle to work, the following assumptions must be satisfied:

There should be a steady-state flow (the fluid’s properties do not change over time).
There should be an in-compressible flow (the density must be constant).
There should be frictionless flow.
The fluid should flow along the streamline, and the flow lines must not intersect.

Hagen-Poiseuille Equation:

Defines flow rate for laminar flow in a pipe, where flow rate is directly proportional to the pressure difference and inversely proportional to fluid viscosity and pipe length.

Darcy-Weisbach Equation:

Relates pressure drop to flow rate in turbulent flow conditions, taking into account pipe roughness and friction factors.

What Is A Pressure Drop?

Technically and economically, the pressure drop (or pressure loss) indicates how much power the gadget needs to operate. It is the total fluid differential pressure between the device’s inlet and outlet.

Pressure drop is the decrease in pressure from one point in a pipeline or fluid system to another, caused by friction or resistance to flow.
The pressure loss experienced by the fluid as it moves through a straight conduit is known as the along-range pressure drop.

The term “local pressure drop” describes the loss of pressure due to alterations to the flow cross-section as the liquid passes through a valve opening, an elbow, or some other local resistance.

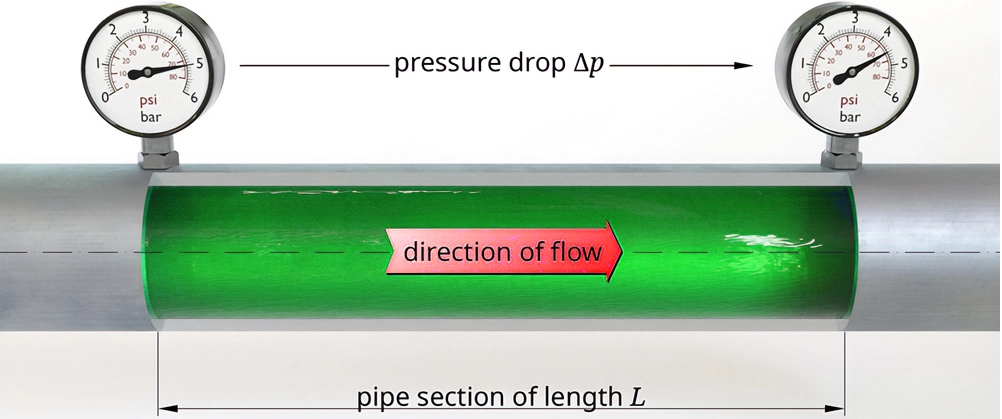
Effects of Pressure Drop on Flow Rate

A pressure drop occurs when a fluid moves through a restriction, frictional resistance, or elevation changes in a pipeline. As pressure decreases, the velocity of the fluid must increase to maintain mass continuity, affecting flow rate measurements. High-pressure drops can lead to inefficiencies, energy losses, and potential damage to equipment.

Coriolis Flow Meter Pressure Drop

Causes of Pressure Drop in Coriolis Flow Meters

Despite their accuracy, Coriolis meters introduce a pressure drop in the system due to:

The bending and vibration of the tubes that create flow resistance.
The meter’s internal diameter, which may be smaller than the pipeline’s diameter, increasing velocity and causing pressure loss.
Higher fluid viscosity, which increases resistance and further contributes to pressure drop.

Mitigating Pressure Drop in Coriolis Meters

Choose a meter with a larger diameter to reduce velocity changes.
Install the meter in a straight, non-restrictive section of the pipeline.
Use a bypass system if pressure drop needs to be reduced while maintaining accuracy.

Pressure Drop in Orifice Plates

Factors Influencing Pressure Drop in Orifice Plates:

Orifice Plate Diameter: Smaller openings create larger pressure drops.
Flow Velocity: Higher velocity increases the pressure differential.
Fluid Properties: Viscosity and density affect the extent of pressure loss.
Beta Ratio: The ratio of orifice diameter to pipe diameter impacts efficiency; lower ratios lead to greater pressure drops.

Pressure Drop Calculations: Key Considerations

Pressure drop is commonly estimated using empirical equations such as:

Darcy-Weisbach Equation: Applicable for both laminar and turbulent flow.

The relationship between flow rate and pressure drop can be described by the Darcy-Weisbach equation, which relates the pressure drop to the pipe diameter, fluid density, flow velocity, and friction factor:

ΔP = f (L/D) (ρV^2/2)

where:
ΔP = pressure drop
f = friction factor
L = length of pipe
D = pipe diameter
ρ = fluid density
V = flow velocity

The equation shows that the pressure drop is proportional to the square of the flow velocity. Therefore, increasing the flow rate will result in a larger pressure drop, which can be problematic if the pressure drop is too large and affects the system’s performance.

Orifice Equation: Used for flow restriction devices like orifice plates.

Flow Coefficients (Cv and Kv): Used in valve and instrumentation sizing.

Reducing Pressure Drop While Maintaining Flow Accuracy

Select appropriate flow meters based on fluid properties and operational needs.
Optimize pipeline design to reduce bends, fittings, and abrupt diameter changes.
Use low-resistance flow meters such as ultrasonic or electromagnetic meters where applicable.